幾何寶庫

 
難度：☆☆☆
題目：
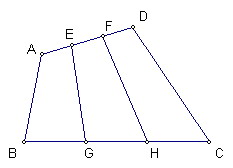
如圖,四邊形ABCD中
E、F在AD上使得AE=EF=FD
G、H在BC上使得BG=GH=HC
試證明四邊形EFHG面積=1/3*四邊形ABCD面積
看解答請點此

 
難度：☆☆☆
題目：
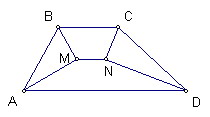
梯形ABCD中AD平行BC
M為∠A和∠B的角平分線交點
N為∠C和∠D的角平分線交點
試證明|AD+BC-AB-CD|=2MN
看解答請點此

 

難度：☆☆☆☆☆

題目：
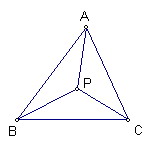
P為△ABC內一點
且∠BPC-∠BAC=∠APB-∠ACB=∠CPA-∠CBA
試證明PB*AC=PC*AB=PA*BC

看解答請點此

 
難度：☆☆☆
題目：
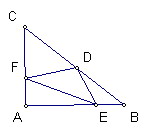
直角三角形ABC中∠A為直角
D為BC中點
E、F分別為AB、AC上的點
證明DE+DF+EF>BC
看解答請點此

 
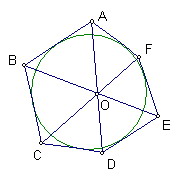
定理內容：
連接外切圓的六邊形ABCDEF的相對頂點的三條對角線AD、BE、CF共點
此定理也叫布里昂雄定理
定理證明：
 
先看引理
若P'、Q'是圓O在P、Q處切線上的點且在PQ同側
若PP'=QQ'
則存在一個圓與PP'、QQ'相切於P'、Q'
以下是引理證明
作PQ的中垂線L
則整個圖形關於L對稱
從而過點P'、Q'的垂線交L於同一點O'
以O'為圓心O'P'為半徑的圓則會與PP'、QQ'切於P、Q
引理得證
接著要來證明Brianchon定理
 
如圖ABCDEF是圓外切六邊形
R、Q、T、S、P、U為切點
在PF、QB、RB、SD、TD、UF延長線分別取點P'、Q'、R'、S'、T'、U'
使得PP'=QQ'=RR'=SS'=TT'=UU'
由引理存在圓Ⅰ與PP'、QQ'切於P'、Q'
存在圓Ⅱ與RR'、SS'切於R'、S'
存在圓Ⅲ與TT'、UU'切於T'、U'
又由切線性質可知AR=AU、DT=DS
所以有AR'=AU'、DS'=DT'
即AD為圓Ⅱ和圓Ⅲ的等冪軸
同理BE為圓Ⅰ和圓Ⅱ的等冪軸、CF為圓Ⅰ和圓Ⅲ的等冪軸
設AD、BE交於O
則O與圓Ⅰ、圓Ⅱ等冪、與圓Ⅱ、圓Ⅲ等冪
即O在CF上
故AD、BE、CF交於一點O
得證

 
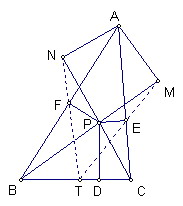
難度：☆☆☆☆☆
題目：
P為△ABC內部一點
D、E、F分別為P到BC、AC、AB的垂足
AM垂直垂直PB於M
AN垂直直線PC於N
試證明ME、NF、BC三直線共點
看解答請點此

 
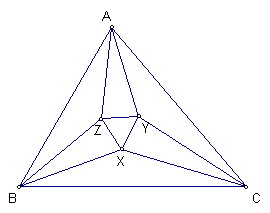
定理內容：
將任意三角形的各角三等分
則與每邊相鄰的兩條三等分線的交點構成一個正三角形
此定理也叫莫利定理
定理證明：
 
如圖，設△ABC的∠A=3α,∠B=β,∠C=γ
與BC相鄰的兩條三等分分角線交於X
∠B和∠C的另兩條三等分分角線交於S
則X為△SBC的內心
從而XS平分∠BSC
在SX兩側分別作∠SXZ=∠SXY=30°
且Z、Y分別在BS、CS上
則△SXZ全等於△SXY
所以XZ=XY
又∠ZXY=60°
故△XYZ為正三角形
接下來要證AZ、AY三等分∠A
分別在BA、CA取BX'=BX,CX"=CX
則△BZX'全等於△BZX
從而ZX'=ZX=ZY
同理有YX"=ZY
所以X'Z=ZY=YX"
∠X'ZY=360°-2∠BZX-60°
=360°-2(∠S/2+30°)-60°
=240°-∠S
=240°-(180°-2β-2γ)
=60°+2(β+γ)
=60°+2(60°-α)
=180°-2α
同理∠ZYX"=180°-2α
作X'ZY的外接圓O由對稱性知X"也在圓O上
易證明圓心角∠X'OZ=∠ZOY=∠YOX"=2α
故∠X'OX"=6α
又因為∠A=3α
故A也在圓O上
又弦X'Z=ZY=YX"
得AZ、AY為∠A的三等分線
故得證

 
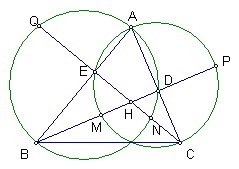
難度：☆☆☆
題目：
銳角△ABC中BD、CE分別為AC、AB上的高
△AEC和△ADB的外接圓分別交BD、CE於M、N
延長BD、CE交圓於P、Q
證明P,Q,M,N四點共圓
看解答請點此

 
難度：☆☆
題目：
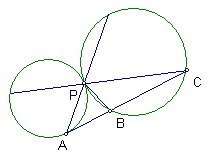
如圖,設有兩圓相切於P
其中一圓的切線切圓於A且交另一圓於B、C兩點
試證明PA為∠BPC的外角平分線
看解答請點此

難度：☆☆☆

題目：
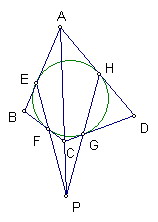
四邊形ACBD的內切圓分別切AB、BC、CD、DA於E、F、G、H
試證明直線EF、GH、AC三線共點

看解答請點此