幾何寶庫

 
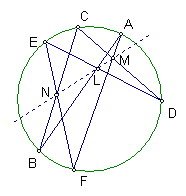
定理內容：
圓上六點A、B、C、D、E、F
AB和DE交點為L
CD和AF交點為M
BC和EF交點為N
則L、M、N三點共線
此定理也叫帕斯卡定理、巴斯卡定理
定理證明：
 
如圖，直線CD、直線EF交於U
直線AB交直線CD、直線EF於W、V
直線DE、AF、BC分別截△UVW
由Menelaus定理有
VL/LW*WD/DU*UE/EV=1......(1)
VA/AW*WM/MU*UF/FV=1......(2)
VB/BW*WC/CU*UN/NV=1......(3)
由圓冪定理可得
WD/DU*UE/EV*VA/AW*UF/FV*VB/BW*WC
=(UE*UF)/(UC*UD)*(VA*VB)/(VE*VF)*(WC*WD)/(WA*WB)=1
(1)*(2)*(3)得VL/LW*WM/MU*UN/NV=1
由Menelaus逆定理得L、M、M三點共線
得證

 

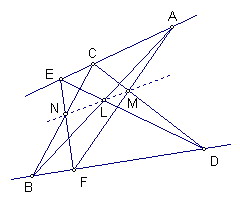
定理內容：
設A、C、E是一直線上三點,B、D、F是另一直線上三點
如果AB、CD、EF分別與DE、FA、BC相交
則三個交點L、M、N三點共線
此定理也叫帕普斯定理

定理證明：

 

如圖，設直線CD與直線EF交於U
直線AB交直線CD、EF於W、V

運用Menelaus定理
△UVW有五條截線AF、BC、AC、BF、DE
可得以下五式
VL/LW*WD/DU*UE/EV=1......(1)
VA/AW*WM/MU*UF/FV=1......(2)
VB/BW*WC/CU*UN/NV=1......(3)
VA/AW*WC/CU*UE/EV=1......(4)
CB/BW*WD/DU*UF/FV=1......(5)

[(1)*(2)*(3)]/[(4)*(5)]可得
VL/LW*WM/MU*UN/NV=1

由Menelaus逆定理可得L、M、N三點共線

得證

 
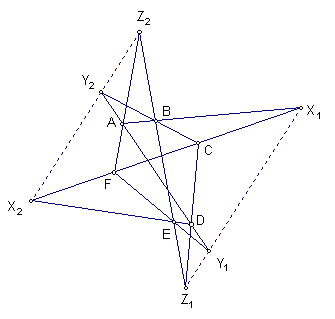
難度：☆☆☆☆
題目：
六邊形ABCDEF對邊兩兩平行
直線CF交AB、DE延長線於X1、X2
直線AD交FE、BC延長線於Y1、Y2
直線BE交CD、AF延長線於Z1、Z2
試證明若X1、Y1、Z1三點共線
則X2、Y2、Z2三點也共線且直線X1Y1Z1平行X2Y2Z2
看解答請點此

 
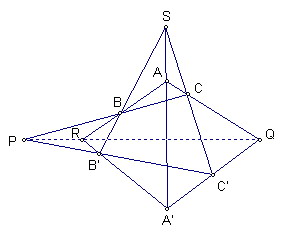
定理內容：
若兩個三角形對應頂點的連線共點
則其對應邊的交點共線
此定理也叫笛沙格定理、戴沙格定理
定理證明：
 
如圖，△ABC和△A'B'C'其對應頂點連線AA'、BB'、CC'交於一點S
BC與B'C'交於P、AC與A'C'交於Q、AB與A'B'交於R
由直線PB'C'截△SBC
由Menelaus定理有
BP/PC*CC'/C'S*SB'/B'B=1
同理由直線QC'A'截△SCA有
CQ/QA*AA'/A'S*SC'/C'C=1
由直線RB'A截△SAB有
AR/RB*BB'/B'S*SA'/A'A=1
以上三式相乘即得BP/PC*CQ/QA*AR/RB=1
由Menelaus逆定理得P、Q、R三點共線
得證
逆定理內容：
若兩個三角形對應邊的交點共線
則他們對應頂點的連線共點
逆定理證明：
  
如圖，△ABC和△A'B'C對應邊交點P、Q、R共線
BB直線、AA直線交於S
由直線SCC'截△SBC
由Menelaus定理有
QC'/C'A'*A'S/SA*AC/CQ=1
同理由直線PRQ截△A'B'C'有
A'C'/C'Q*QP/PR*RB'/B'A'=1
由直線PBC截△AQR有
AB/BR*RP/PQ*QC/CA=1
以上三式相乘有
RB'/B'A'*A'S/SA*AB/BR=1
由Menelaus逆定理得S、B、B'三點共線
即AA'、BB'、CC'交於一點S
得證

 
定理內容：
以三角形各邊為邊分別向外側作正三角形
則三個正三角形的中心構成一個正三角形
此定理也叫拿破崙定理
定理證明：
 
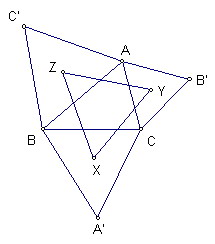
如圖△A'BC、△AB'C、△ABC'是以△ABC三邊向外作的三個正三角形
X、Y、Z分別為三正三角形的中心
連AA'、BB'、CC'
∵AB'=AC,AC'=AB,∠CAC'=∠BAB'
∴△BAB'全等於△C'AC(SAS)
→BB'=CC'
同理可得AA'=BB'
所以AA'=BB'=CC'
BZ=√3/3*AB,BX=√3/3*BC
∵BZ/BX=AB/BC=BC'/BC,∠ZBX=∠C'BC
∴△ZBX全等於△C'BC(SAS)
→XZ/CC'=√3/3
同理XY/AA'=YZ/BB'=√3/3
故XY=YZ=XZ
即△XYZ為正三角形
得證

 
定理內容：
兩條內角平分線等長的三角形為等腰三角形
此定理也叫斯坦納-雷米歐司定理
定理證明：
 
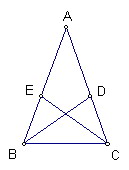
如圖BD、CE都為角平分線
設BC=a,AB=c,AC=b
由於BD、CE都為角平分線
得AD=bc/(a+c),CD=ab/(a+c),AE=bc/(a+b),BE=ac/(a+b)
由Schooten定理得
BD^2=AB*BC-AD*DC=ac-bc/(a+c)*ab/(a+c)
CE^2=AC*BC-AE*EB=ab-bc/(a+b)*ac/(a+b)
又BD=CE
故ac-bc/(a+c)*ab/(a+c)=ab-bc/(a+b)*ac/(a+b)
整理得
(b-c)(a^3+a^2*b+a^2*c+3abc+b^2*c+c^2*b)=0
顯然b-c=0
即△ABC為等腰三角形
得證

 
定理內容：
正三角形內任意點到三邊的距離之和為定值：三角形的高
此定理也叫維維安尼定理
定理證明：
 
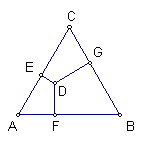
如圖設正三角形ABC內部一點D到三邊的距離為DE、DF、DG
可設△的邊長為a
△ABC面積=△ACD面積+△ABD面積+△BCD面積
=1/2*AC*DE+1/2*AB*DF+1/2*BC*DG
=1/2*a*(DE+DF+DG)
→DE+DF+DG=2*△ABC面積/a=三角形的高 為定值
得證

 
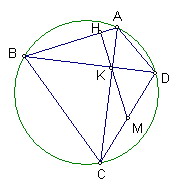
定理內容：
內接於圓的四邊形ABCD的對角線AC、BD垂直相交於K
過K的直線與AB、CD分別相交於H、M
(1)如果KH⊥AB,則MC=MD
(2)如果MC=MD,則KH⊥AB
此定理也叫婆羅摩及多定理、布拉美古塔定理
定理證明：
 
(1)
∵KH⊥AB、AC⊥BD
∴∠1=∠2=∠4
又∠2=∠3
所以∠3=∠4
→MC=MK
同理MD=MK
即MC=MD
得證
(2)
由MC=MD
得知KM為直角三角形CKD斜邊CD上中線
因此有MK=MC
→∠3=∠4
又∠3=∠2,∠4=∠1
所以∠2=∠1
而∠1+∠5=90°
所以∠2+∠5=90°
即KH⊥AB
得證
逆定理內容：
若四邊形的對角線互相垂直,並且
(1)過對角線交點向一邊所做垂線平分其對邊
(2)對角線交點與一邊中點的連線垂直於對邊
(3)對角線交點、交點在一邊上的射影及對邊中點三點共線
這三個中只要一個成立,則四邊形內接於圓
逆定理證明：
 
(1)
如圖,設KT⊥AD,KH⊥AB
HK、TK分別交CD、BC於M、N且M、N分別為CD、BC中點
則可得∠1=∠2=∠3,∠5=∠6=∠7
∵∠4+∠3=90°,∠8+∠7=90°
∴∠4+∠1=90°,∠8+∠5=90°
→∠CBA+∠CDA=180°
→四邊形ABCD內接於圓
得證
(2)
如圖，設M、N分別為CD、BC中點
MK、NK分別交AB、AD於H、T且KH⊥AB、KT⊥AD
則可得∠1=∠2=∠3,∠5=∠6=∠7

 
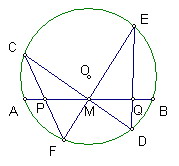
定理內容：
過圓O中AB中點M引任意兩弦CD、EF
CF、ED分別交AB於P、Q
則MP=MQ
定理證明：
 
設PM=x,MQ=y,AM=BM=a
過P分別作CD、EF垂線其垂足為G、H
過Q分別作CD、EF垂線其垂足為K、L
x/y=PG/QK=PH/QL
→(x/y)^2=PG/QK*PH/QL=PG/QL*PH/QK
又易證△PCG相似△QEL
可得PG/QL=PC/QE
同理PH/QK=PF/QD
→(x/y)^2=PC/QE*PF/QD=(PC*PF)/(QE*QD)=(AP*PB)/(BQ*QA)
→(x/y)^2=[(a+x)(a-x)]/[(a+y)(a-y)]
→x=y
即MP=MQ
得證

 
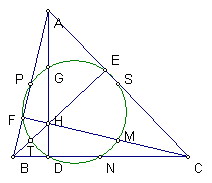
定理內容：
三角形三條高的垂足、三邊中點、以及垂心與頂點的三條連接線段的中點
這九點共圓
定理證明：
 
如圖，AD、BE、CF為△ABC的高,垂心為H
N、P、S為三邊中點,G、T、M分別為AH、BH、CH中點
PS//TM//BC且PS=1/2*BC=TM
PT//SM//AH且PT=1/2*AH=SM
又AD⊥BC
故四邊形PTMS為矩形
同理四邊形TNSG也為矩形
顯然P,T,M,S,N,G都在直徑為TS的圓上
又∠GDN=90°
所以D也在此圓上
同理E、F也在此圓上
即D、E、F、G、T、M、N、S、P九點共圓
得證