幾何寶庫

 
定理內容：
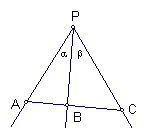
共線的三點A、B、C依次分別是平面一點P所引三條射線PA、PB、PC上的點
線段AC、CB對P的張角分別為α、β且α+β<180°
則sin(α+β)/PB=sinα/PC+sinβ/PA
定理證明：
△PAC面積=△PAB面積+△PBC面積
→1/2*PA*PC*sin(α+β)=1/2*PA*PB*sinα+1/2*PB*PC*sinβ
→sin(α+β)/PB=sinα/PC+sinβ/PA
得證
逆定理內容：
A、B、C依次分別是平面一點P所引三條射線PA、PB、PC上的點
線段AC、CB對P的張角分別為α、β且α+β<180°
若sin(α+β)/PB=sinα/PC+sinβ/PA
則A、B、C三點共線
逆定理證明：
sin(α+β)/PB=sinα/PC+sinβ/PA
→1/2*PA*PC*sin(α+β)=1/2*PA*PB*sinα+1/2*PB*PC*sinβ
→△PAC面積=△PAB面積+△PBC面積
故A、B、C三點共線
得證

 
難度：☆☆☆☆
題目：
S為銳角三角形ABC中AB上的點
P、Q分別為△ASC、△BSC的外心
求S在AB上的什麼位置時△PQS面積最小
看解答請點此

 
難度：☆☆☆☆
題目：
已知X是△ABC中AB上的一點
P為△ACX內心,Q為△BCX內心,M為PQ中點
試證明MC>MX
看解答請點此

 
定理內容：
過三角形外接圓上任意一點作三邊直線的垂線
則三垂足點共線
此定理也叫西姆松定理、西摩松定理
定理證明：
 
如圖，從P點引出三條垂線其BC、AC、AB的垂足分別為L、M、N
連PA、PC
可得A,N,P,M四點共圓、P,M,L,C四點共圓
∠NMA=90°-∠NMP=90°-∠NAP=90°-∠BCP=∠LPC=∠LMC
即L、M、N共線
得證
逆定理內容：
若一點在三角形三邊所在直線上的射影共線
則該點在此三角形的外接圓上
逆定理證明：
  
如圖
設P對BC、AC、AB的射影分別為L、M、N且L、M、N共線
連PA、PB
可得A,N,P,M四點共圓、P,A,B,L四點共圓
∠PAC=∠PAM=∠PNM=∠PNL=∠PBL=∠PBC
得P、A、B、C四點共圓
即P在ABC外接圓上
得證

 
難度：☆☆☆
題目：
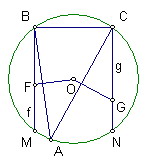
A,B,C是圓O上三個相異的點
過B,C作BC的垂線f和g
AB中垂線交f於F
AC中垂線交g於G
證明不論A,B,C怎麼取,BF*CG都為定值
看解答請點此

 
難度：☆☆
題目：
△ABC中D在BC上
且BD：CD=m：n
試證明n*AB+m*AC>(m+n)*AD
看解答請點此

 
難度：☆☆
題目：
如圖,矩形ABCD,延長BC至E使得CA=CE
AE中點F,連DF、BF
試證明DF⊥BF
看解答請點此

 
難度：☆☆☆
題目：
△ABC中,∠B>∠C
∠A的角平分線交BC於D
在BC上取一點E使得BE=CD
試證明(AC-AB)^2=AE^2-AD^2
看解答請點此

 
難度：☆☆☆☆
題目：
正△ABC內部有一點P
射線AP、BP、CP依次交BC、AC、AB於D、E、F
試證明DE*EF*FD≧CD*BF*AE
看解答請點此

 
難度：☆☆☆
題目：
如圖,D在△ABC內部,過D做AB、BC、AC垂線
並分別在三條線上取E、F、G使得AE=AG,BE=BF
試證明CF=CG
看解答請點此