幾何寶庫

 
定理內容：
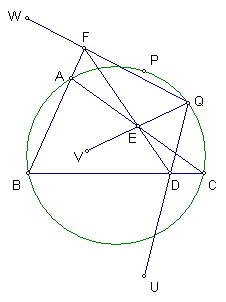
設P、Q為△ABC外接圓上異於A、B、C的任意兩點
P點關於BC、CA、AB的對稱點分別為U、V、W
QU、QV、QW和BC、CA、AB分別交於D、E、F
則D、E、F三點共線
定理證明：
 
∵W、U分別為P關於AB、BC的對稱點
∴∠WAF=∠PAF,∠UCB=∠PCB,PC=CU,PA=AW
∵P,A,B,C和Q,A,B,C共圓
∴∠PAF=∠PCB,∠QAF=∠QCB
所以∠QAW=∠QAF+∠WAF=∠QCB+∠PAF=∠QCB+∠PCB=∠QCB+∠UCB=∠QCU
即△QCU面積/△QAW=(QC*CU)/(QA*AW)=(QC*PC)/(QA*PA)
同理得
△QBW面積/△QCV面積=(QB*PB)/(QC*PC)
△QAV面積/△QBU面積=(QA*PA)/(QC*PC)
CD/BD*BF/AF*AE/CE
=△QCU面積/△QBU面積*△QBW面積/△QAW面積*△QAV面積/△QCV面積
=(QC*PC)/(QA*PA)*(QA*PA)/(QC*PC)*(QB*PB)/(QC*PC)
=1
由Menelaus逆定理得D、E、F三點共線
得證

  
定理內容：
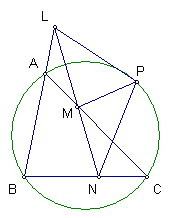
從三角形ABC外接圓上一點P向BC、AC、AB引線段PL、PM、PN成同向等角
則L、M、N三點共線
此定理也叫卡諾定理
當三個角都為90°時,即為Simson定理
定理證明：
  
∵∠PNA=∠PMC=∠PLC
可得A,N,P,M四點共圓、P,M,L,C四點共圓、P,L,A,B四點共圓
∠NMA=∠AMP-∠NMP=∠AMP-∠NAP=∠BLP-∠BCP=∠LPC=∠LMC
即L、M、N共線
得證
逆定理內容：
若△ABC所在平面上一點P對BC、AC、AB引線段PL、PM、PN成同向等角
且L、M、N共線
則P在△ABC外接圓上
逆定理證明：
  
∵∠PNA=∠PMC=∠PLC
可得A,N,P,M四點共圓、P,M,L,C四點共圓、P,L,A,B四點共圓
∠PAC=∠PAM=∠PNM=∠PNL=∠PBL=∠PBC
得P、A、B、C四點共圓
即P在ABC外接圓上
得證

 
難度：☆☆☆
題目：
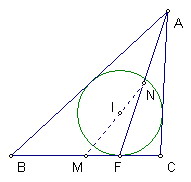
△ABC的內切圓切BC於F,內切圓圓心為I
M、N分別為BC、AF中點
試證明N、I、M共線
看解答請點此

 
難度：☆☆☆☆
題目：
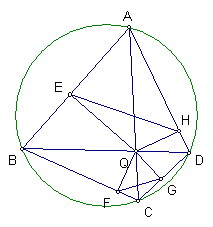
四邊形ABCD內接於圓
對角線AC和BD交點為Q
Q對AB、BC、CD、DA做垂線的垂足分別為E、F、G、H
試證明直線FG、直線EH、直線BD平行或共點
看解答請點此

 

難度：☆☆☆☆

題目：
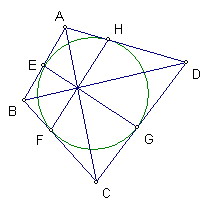
四邊形ABCD外切於一圓
其AB、BC、CD、DA上的切點分別為E、F、G、H
證明AC、BD、EG、FH共點

看解答請點此

 
難度：☆☆☆☆
題目：
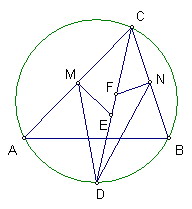
△ABC中∠C的角平分線交外接圓於D
M、N分別為AC、BC的中點
AC和BC的中垂線分別交CD於E、F
試證明△DME和△DNF面積相等
看解答請點此

  
難度：☆☆☆☆
題目：
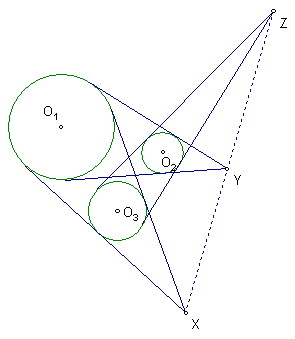
圓O1、圓O2、圓O3是三個半徑不相同的圓
圓O1和圓O2外公切線交點為Y
圓O1和圓O3外公切線交點為X
圓O2和圓O3外公切線交點為Z
試證明X、Y、Z三點共線
看解答請點此

 
難度：☆☆☆☆☆
題目：
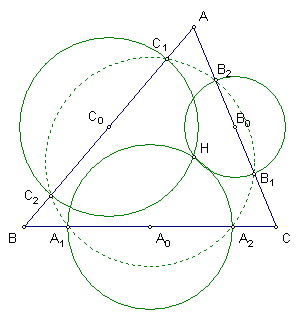
如圖,已知H是銳角三角形ABC的垂心
已BC邊中點A0為圓心,過H的圓交BC於A1、A2
已CA邊中點B0為圓心,過H的圓交CA於B1、B2
已AB邊中點C0為圓心,過H的圓交BC於C1、C2
證明A1、A2、B1、B2、C1、C2六點共圓
看解答請點此

 
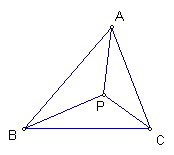
Fermat點(費瑪點)：
△ABC三內角都小於120°
則平面上一點P使得PA+PB+PC的值最小的P點稱作Fermat點
此時∠APB=∠BPC=∠CPA=120°
證明：
 
如圖,∠APB=∠BPC=∠CPA=120°
分別過A、B、C作PA、PB、PC的垂線
三線交於D、E、F
∵∠APB=∠BPC=∠CPA=120°
∴∠AFB=∠BDC=∠CEA=60°
→△DEF為正三角形
M為平面上一點
過M作△DEF三邊垂線其垂足為Q、R、S
由Viviani定理可得PA+PB+PC=MQ+MR+MS
∵∠MQA=∠MRB=∠MSC=90°
∴MA+MB+MC≧MQ+MR+MS=PA+PB+PC
等號在M點和P點重合時成立
得證

 
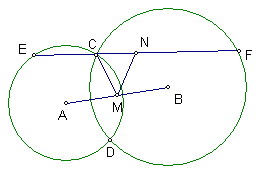
難度：☆☆☆
題目：
圓A和圓B相交於C、D
過C做一直線分別交圓A、圓B於E、F
M、N分別為EF、AB中點
證明MN=MC
看解答請點此