幾何寶庫

 
定理內容：
任意四邊形ABCD中，對角線AD、BC
則AB*CD+BC*AD≧AC*BD
定理證明：
 
在四邊形ABCD內取一點E使得∠BAE=∠CAD,∠ABE=∠ACD
則△ABE～△ACD(AA)
→AB/BE=AC/CD
→AB*CD=AC*BE
∵AD/AC=AE/AB→AD/AE=AC/AB且∠BAC=∠EAD
∴△ABC～△AED
→AD/DE=AC/BC
→BC*AD=AC*DE
AB*CD+BC+AD=AC*BE+AC*DE
=AC(BE+DE)
≧AC*BD
等號成立時僅當E在BD上,即∠ABD=∠ACD,此時A、B、C、D四點共圓
得證

 
定理內容：
任意三角形ABC中
AD為∠A角平分線
則AD^2=AB*AC-BD*CD
此定理也叫斯霍騰定理
定理證明：
 
延長AD交△ABC外接圓於E，連BE
∵∠BAE=∠DAC,∠E=∠C
∴△ABE相似於△ADC
→AB/AD=AE/AC
→AB*AC=AD*AE=AD(AD+DE)=AD^2+AD*DE
又由圓冪定理得
AD*DE=BD*CD
即AD^2=AB*AC-BD*CD
得證

  
定理內容：
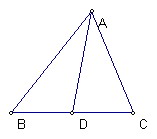
對於任意三角形ABC及邊BC上中點D
則AB^2+AC^2=2(BD^2+AD^2)
此定理也叫Apollonios定理、阿波羅尼奧斯定理、巴布斯定理
定理證明：
 
AC^2=AD^2+CD^2-2*AC*CD*cosθ......(1)
AB^2=AD^2+BD^2+2*AB*BD*cosθ=AD^2+CD^2+2*AB*CD*cosθ......(2)
(1)+(2)→AB^2+AC^2=2(BD^2+AD^2)
得證

 

難度：☆☆☆☆☆☆

題目：
圖中AB為圓O直徑，CD過O且CO=DO
AD延長交圓於E，AC延長交圓於F
EF延長線和CD延長線交於G
試證明GB為圓O切線

看解答請點此

 

難度：☆☆☆

題目：
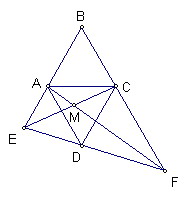
設四邊形ABCD的四邊等長且∠ABC=60°
直線L通過D點且與四邊形不相交(除了D點以外)
並設直線L與直線AB、BC分別交於E、F
且線段CE、AF交於M
試證CA^2=CM*CE

看解答請點此

 
定理內容：
設P為△內部或邊上一點
P到BC、AC、AB的距離為PD、PE、PF
則PA+PB+PC≧2(PD+PE+PF)
此定理也叫厄多斯莫德爾不等式
定理證明：
由餘弦定理得
DE^2=PD^2+PE^2-2*PD*PE*cos(∠EPD)
=PD^2+PE^2-2*PD*PE*cos(A+B)
=(PD*sinB+PE*sinA)^2+(PD*cosB-PE*cosA)^2
≧(PD*sinB+PE*sinA)^2
→DE≧PD*sinB+PE*sinA
由正弦定理和P,E,D,C四點共圓得
DE/sinC=EC/sin(∠EDC)=EC/sin(∠EPC)=PC/sin(∠PEC)=PC
→DE=PC*sinC
∴PC*sinC≧PD*sinB+PE*sinA
→PC≧PD*sinB/sinC+PE*sinA/sinC
∴PA+PB+PC≧PD*(sinB/sinC+sinC/sinB)+PE(sinA/sinC+sinC/sinA)+PF(sinB/sinA+sinA/sinB)
≧2(PD+PE+PF)
得證

定理內容：
在△ABC中
a^2+b^2+c^2≧4√3*S
S表△ABC面積
其等號成立時△ABC為正三角形
定理證明：
a^2+b^2+c^2-4√3*S
=a^2+b^2+c^2-4√3*1/2*bc*sinA
=b^2+c^2-2bc*cosA+b^2+c^2-2√3*bc*sinA
=2(b^2+c^2-2bc*sin(A+30°))
≧2(b^2+c^2-2bc)
=2(b-c)^2
≧0
△ABC為正三角形時等號成立
得證

 

難度：☆☆☆

題目：
A為圓O外一點
AB、AC是圓O的兩條切線
D、E分別在AB、AC延長線上且AE通過O
BE、CD交於F
證明AF垂直DE

看解答請點此

 

難度：☆☆☆

題目：
如圖，過圓外一點M作圓的兩條切線和一條割線
切點為A、B
所作之割線交圓於C、D且C在M、D之間
在CD上取一點N使得∠DAN=∠MBC
證明∠DBN=∠MAC

看解答請點此

 

難度：☆☆☆

題目：
如圖，O為圓內接四邊形ABCD對角線的交點
OE⊥AB,OF⊥CB,OG⊥CD,OH⊥AD
求證EH+GF=EF+GH

看解答請點此