
難度:☆☆☆
題目:
如圖,線段PD⊥AB且AB=PD
D在AB上,H為△PAB的垂心
C為AB中點
試證明不論D點在哪CH+DH皆為定值
看解答請點此
ej0cl6 發表在 痞客邦 留言(0) 人氣(187)
公式內容:
在四邊形ABCD中
AB=a,BC=b,CD=c,DA=d
設p=(a+b+c+d)/2
且∠A+∠C=2θ
則此四邊形面積=[(p-a)(p-b)(p-c)(p-d)-4abcd*cos^2θ]^(1/2)
公式證明:
設S為四邊形ABCD面積
△ABD面積=1/2*ad*sinA
△CBD面積=1/2*bc*sinC
S=1/2(ad*sinA+bc*sinC)
4S^2=(ad*sinA+bc*sinC)^2
由餘弦定理得
BD^2=a^2+d^2-2ad*cosA=b^2+c^2-2bc*cosC
ad*cosA-bc*cosC=-1/2*(b^2+c^2-a^2-d^2)
4S^2+1/4*(b^2+c^2-a^2-d^2)^2
=(ad*sinA+bc*sinC)^2+(ad*cosA-bc*cosC)^2
=(ad)^2+(bc)^2-2abcd*cos2θ
=(ad)^2+(bc)^2-2abcd*(2cos^2θ-1)
=(ad+bc)^2-4abcd*cos^2θ
16S^2
=4(ad+bc)^2-(b^2+c^2-a^2-d^2)^2-16abcd*cos^2θ
=16(p-a)(p-b)(p-c)(p-d)-16abcd*cos^2θ
即S=[(p-a)(p-b)(p-c)(p-d)-4abcd*cos^2θ]^(1/2)
得證
ej0cl6 發表在 痞客邦 留言(1) 人氣(756)
公式內容:
對於任意△ABC
△ABC面積=[s(s-a)(s-b)(s-c)]^(1/2)
恆成立 其中s=(a+b+c)/2
此公式也叫海龍公式
公式證明:
設△ABC面積為x
x^2=(1/2*ab*sinC)^2
=1/4*a^2*b^2*sin^2C
=1/4*a^2*b^2(1-cos^2C)
=1/4*a^2*b^2-1/4*a^2*b^2*cos^2C
=1/4*a^2*b^2-1/4*a^2*b^2*[(a^2+b^2-c^2)/(2ab)]^2
=1/16*(2ab)^2-1/16*(a^2+b^2-c^2)
=1/16*(2ab+a^2+b^2-c^2)(2ab-a^2-b^2+c^2)
=1/16*[(a+b)^2-c^2][c^2-(a+b)^2]
=1/16*(a+b+c)(a+b-c)(a-b+c)(b+c-a)
=s(s-a)(s-b)(s-c)
兩邊開根號即得x=[s(s-a)(s-b)(s-c)]^(1/2)
得證
ej0cl6 發表在 痞客邦 留言(0) 人氣(850)

定理內容:
對於任意△ABC
a^2=b^2+c^2-2bc*cosA
b^2=a^2+c^2-2ac*cosB
c^2=a^2+b^2-2ab*cosC
恆成立
定理證明:
如圖
對△ABC三邊向外做正方形ABIH、BCGF、ACED
AL⊥FG、BK⊥DE、CJ⊥IH
由三角函數定義可得
BN=c*cosB,BM=a*cosB
長方形BMJI面積=c*a*cosB=長方形BNLF面積
同理
長方形CNLG面積=長方形COKE面積
長方形AMJG面積=長方形AOKD面積
正方形ACDE面積=正方形BCGF面積+正方形ABIH面積-長方形BMJI面積-長方形BNLF面積
即b^2=a^2+c^2-2ac*cosB
同理
a^2=b^2+c^2-2bc*cosA
c^2=a^2+b^2-2ab*cosC
得證
ej0cl6 發表在 痞客邦 留言(0) 人氣(1,179)
定理內容:
對於任意三角形ABC
a/sinA=b/sinB=c/sinC=2R 恆成立
(R為三角形外接圓半徑)
定理證明:
三角形面積可表示成
1/2*b*c*sinA or 1/2*a*c*sinB or 1/2*a*b*sinC
可以得到
1/2*b*c*sinA=1/2*a*c*sinB=1/2*a*b*sinC
同乘以2得
b*c*sinA=a*c*sinB=a*b*sinC
同除以a*b*c得
sinA/a=sinB/b=sinC/c
取倒數即得
a/sinA=b/sinB=c/sinC
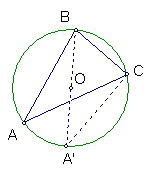
圖中BA'為直徑=2R
∠A'=∠A
sinA=sinA'=BC/BA'=a/(2R)
即2R=a/sinA
以上,得a/sinA=b/sinB=c/sinC=2R
得證
ej0cl6 發表在 痞客邦 留言(0) 人氣(11,398)

難度:☆☆☆
題目:
已知△ABC,G為其重心,M為平面上任一點
求證MA^2+MB^2+MC^2=AG^2+BG^2+CG^2+3MG^2
看解答請點此
ej0cl6 發表在 痞客邦 留言(0) 人氣(174)

難度:☆☆☆
題目:
AD為△ABC的BC邊上中線,G為垂心
過G引直線與AC、AB分別交於E、F
求證:BF/AF+CE/AE=1
看解答請點此
ej0cl6 發表在 痞客邦 留言(0) 人氣(207)
難度:☆☆☆
題目:
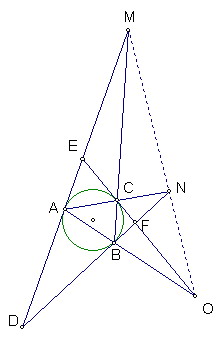
在△ABC的外接圓上,分別過三頂點A,B,C作外接圓的三切線
三切線與三頂點對邊的延長線分別交於M,N,O
試證明M,N,O三點共線
看解答請點此
ej0cl6 發表在 痞客邦 留言(0) 人氣(400)
難度:☆☆☆
題目:
已知兩個圓相內切,切點為A
一條直線依次與這兩個圓交於點M、N、P、Q
求證∠MAP=∠NAQ
看解答請點此
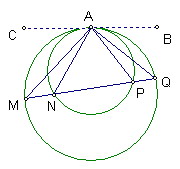
作切線BC
得∠CAN=∠MPN,∠CAM=∠MQN
∠MAN=∠CAN-∠CAM=∠MPN-∠MQN=∠PAQ
∠MAP=∠MAN+∠NAP=∠NAP+∠PAQ=∠NAQ
得證
ej0cl6 發表在 痞客邦 留言(0) 人氣(180)

難度:☆☆☆
題目:
AB為圓的一弦
M為優弧AB中點
C為優弧AB上任一點
MD垂直AC於D
求證BC+CD=AD
看解答請點此
ej0cl6 發表在 痞客邦 留言(0) 人氣(185)







