幾何寶庫

 
難度：☆
題目：
等腰三角形中AB=AC,P為三角形內部任一點
AD、AE分別平分∠BAP、∠CAP
證明DE平行BC
看解答請點此

 
難度：☆☆☆
題目：
A、B、D在同一條直線上
且△ABC和△BDE都是正三角形
F、D分別為CD、AE中點
證明△BFD為正三角形
看解答請點此

 

難度：☆☆☆☆☆

題目：
等腰三角形ABC中,AC=BC且∠C=20°
D在BC上使得∠BAD=50°
E在AC上使得∠ABE=60°
求∠DEB

看解答請點此

 

難度：☆☆☆

題目：
平行四邊形ABCD中,E在AD上,F在CD上
且AE=CF
AF和CE交於G
證明BG平分角ABC

看解答請點此

 
難度：☆☆☆
題目：
△ABC分別向AB、AC外側作平行四邊形ABED、ACGF
設ED延長線、GF延長線交於H
向BC外側作一平行四邊形BCIJ使得CI=AH且CI平行AH
證明四邊形BCIJ面積=四邊形ABED面積+四邊形ACGF面積
看解答請點此

 
難度：☆☆☆
題目：
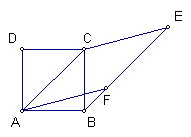
如圖,四邊形ABCD為正方形
四邊形ACEF為菱形且E、F、B共線
證明AF三等分∠BAC
看解答請點此

 
難度：☆☆☆☆☆
題目：
線段AB上有一點C
在AB同側以AB、AC、BC為直徑作三個半圓
AF是兩小圓公切線
D在大圓上且CD⊥AB
證明四邊形CFDE為一矩形
看解答請點此

 
定理內容：
設圓O1、圓O2的半徑分別為r和R，圓心距為d
若存在一個三角形以圓O1為內切圓(或旁切圓)
同時又以內接於圓O2
則d^2=R^2-2Rr　(旁切圓則是d^2=R^2+2Rr)
(此定理的逆定理也成立)
定理證明：
 
連接AO1並延長交圓2於D，連接BD
過O1作圓O2的直徑EF
由圓冪定理有DO1*AO1=EO1*FO1=|R^2-d^2|
又AO1=r/sinα
∠BO1D=β+α=∠O1BD　(旁切圓為∠BO1D=β+α=∠O1BD)
得DO1=BD=2Rsinα
所以AO1*DO1=r/sinα*2Rsinα=2Rr
即|R^2-d^2|=2Rr
當圓O1為內切圓時R>d得d^2=R^2-2Rr
當圓O1為旁切圓時R<d得d^2=R^2+2Rr
得證
逆定理內容：
設圓O1、圓O2的半徑分別為r和R，圓心距為d
若d^2=R^2-2Rr　(或是d^2=R^2+2Rr)
則存在一個△ABC,它外切(或旁切)於圓O1又內接於圓O2
逆定理證明：
  
如圖
在圓O2上任取一點A,延長AO1交圓O2於D
在圓O2上取B、C使DB=DC=DO1
DB=DO1=2Rsinα
DO1*AO1=|R^2-d^2|
代入d^2=R^2-2Rr　(d^2=R^2+2Rr)
化簡得r=AO1*sinα
即sin=r/AO1
故AB為圓O1的切線
同理AC也為圓O1的切線
又因為∠DBO1=∠BO1D=β+α　(β-α)
∠DBC=∠DAC=α
所以∠O1BC=β+α-α　(β-α+α)=β
故BC也為圓O1的切線
即△ABC為所求
得證

  
定理內容：
任意三角形的垂心H、重心G、外心O三點共線
且HG=2GO
定理證明：
 
如圖，設M為AB中點
連接CM，則G在CM上且CG=2GM
連接OM則OM垂直平分AB
延長OG至H'使得H'G=2GO
連接CH'
∵∠CGH'=∠MGO,CG/GM=H'G/GO
∴△CH'G相似於△MGO
→CH'平行OM
即CH'垂直AB
同理，AH垂直BC
即H'為垂心
由於垂心只有一個
因此得證

  

難度：☆☆☆☆

題目：
A,B,C,D,E為正九邊形上連續的五個點
試證明AC/AD=(AD+AB)/(AC+AE)

看解答請點此