close
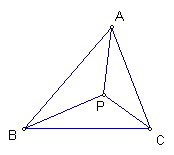
Fermat點(費瑪點):
△ABC三內角都小於120°
則平面上一點P使得PA+PB+PC的值最小的P點稱作Fermat點
此時∠APB=∠BPC=∠CPA=120°
證明: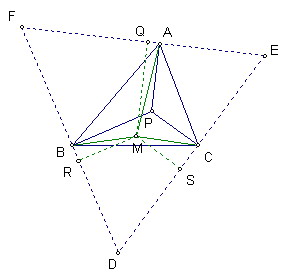
如圖,∠APB=∠BPC=∠CPA=120°
分別過A、B、C作PA、PB、PC的垂線
三線交於D、E、F
∵∠APB=∠BPC=∠CPA=120°
∴∠AFB=∠BDC=∠CEA=60°
→△DEF為正三角形
M為平面上一點
過M作△DEF三邊垂線其垂足為Q、R、S
由Viviani定理可得PA+PB+PC=MQ+MR+MS
∵∠MQA=∠MRB=∠MSC=90°
∴MA+MB+MC≧MQ+MR+MS=PA+PB+PC
等號在M點和P點重合時成立
得證
全站熱搜


 留言列表
留言列表
