close

 a018-1.jpg

定理內容：
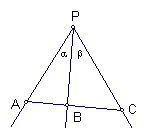
共線的三點A、B、C依次分別是平面一點P所引三條射線PA、PB、PC上的點
線段AC、CB對P的張角分別為α、β且α+β<180°
則sin(α+β)/PB=sinα/PC+sinβ/PA

定理證明：

a018-1.jpg

△PAC面積=△PAB面積+△PBC面積
→1/2*PA*PC*sin(α+β)=1/2*PA*PB*sinα+1/2*PB*PC*sinβ
→sin(α+β)/PB=sinα/PC+sinβ/PA

得證


逆定理內容：
A、B、C依次分別是平面一點P所引三條射線PA、PB、PC上的點
線段AC、CB對P的張角分別為α、β且α+β<180°
若sin(α+β)/PB=sinα/PC+sinβ/PA
則A、B、C三點共線

逆定理證明：

a018-1.jpg

sin(α+β)/PB=sinα/PC+sinβ/PA
→1/2*PA*PC*sin(α+β)=1/2*PA*PB*sinα+1/2*PB*PC*sinβ
→△PAC面積=△PAB面積+△PBC面積

故A、B、C三點共線

得證



arrow
arrow
    全站熱搜

    ej0cl6 發表在 痞客邦 留言(0) 人氣()

    E-mail轉寄