close
定理內容:
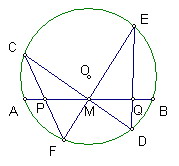
過圓O中AB中點M引任意兩弦CD、EF
CF、ED分別交AB於P、Q
則MP=MQ
定理證明:
設PM=x,MQ=y,AM=BM=a
過P分別作CD、EF垂線其垂足為G、H
過Q分別作CD、EF垂線其垂足為K、L
x/y=PG/QK=PH/QL
→(x/y)^2=PG/QK*PH/QL=PG/QL*PH/QK
又易證△PCG相似△QEL
可得PG/QL=PC/QE
同理PH/QK=PF/QD
→(x/y)^2=PC/QE*PF/QD=(PC*PF)/(QE*QD)=(AP*PB)/(BQ*QA)
→(x/y)^2=[(a+x)(a-x)]/[(a+y)(a-y)]
→x=y
即MP=MQ
得證
全站熱搜


 留言列表
留言列表
