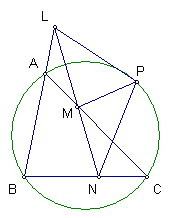
定理內容:
從三角形ABC外接圓上一點P向BC、AC、AB引線段PL、PM、PN成同向等角
則L、M、N三點共線
此定理也叫卡諾定理
當三個角都為90°時,即為Simson定理
定理證明:
∵∠PNA=∠PMC=∠PLC
可得A,N,P,M四點共圓、P,M,L,C四點共圓、P,L,A,B四點共圓
∠NMA=∠AMP-∠NMP=∠AMP-∠NAP=∠BLP-∠BCP=∠LPC=∠LMC
即L、M、N共線
得證
逆定理內容:
若△ABC所在平面上一點P對BC、AC、AB引線段PL、PM、PN成同向等角
且L、M、N共線
則P在△ABC外接圓上
逆定理證明:
∵∠PNA=∠PMC=∠PLC
可得A,N,P,M四點共圓、P,M,L,C四點共圓、P,L,A,B四點共圓
∠PAC=∠PAM=∠PNM=∠PNL=∠PBL=∠PBC
得P、A、B、C四點共圓
即P在ABC外接圓上
得證
全站熱搜


 留言列表
留言列表
