close
定理內容:
將任意三角形的各角三等分
則與每邊相鄰的兩條三等分線的交點構成一個正三角形
此定理也叫莫利定理
定理證明:
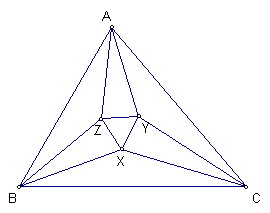
如圖,設△ABC的∠A=3α,∠B=β,∠C=γ
與BC相鄰的兩條三等分分角線交於X
∠B和∠C的另兩條三等分分角線交於S
則X為△SBC的內心
從而XS平分∠BSC
在SX兩側分別作∠SXZ=∠SXY=30°
且Z、Y分別在BS、CS上
則△SXZ全等於△SXY
所以XZ=XY
又∠ZXY=60°
故△XYZ為正三角形
接下來要證AZ、AY三等分∠A
分別在BA、CA取BX'=BX,CX"=CX
則△BZX'全等於△BZX
從而ZX'=ZX=ZY
同理有YX"=ZY
所以X'Z=ZY=YX"
∠X'ZY=360°-2∠BZX-60°
=360°-2(∠S/2+30°)-60°
=240°-∠S
=240°-(180°-2β-2γ)
=60°+2(β+γ)
=60°+2(60°-α)
=180°-2α
同理∠ZYX"=180°-2α
作X'ZY的外接圓O由對稱性知X"也在圓O上
易證明圓心角∠X'OZ=∠ZOY=∠YOX"=2α
故∠X'OX"=6α
又因為∠A=3α
故A也在圓O上
又弦X'Z=ZY=YX"
得AZ、AY為∠A的三等分線
故得證
全站熱搜


 留言列表
留言列表
