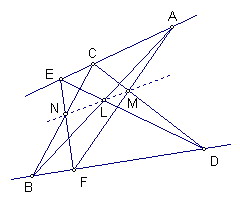
定理內容:
設A、C、E是一直線上三點,B、D、F是另一直線上三點
如果AB、CD、EF分別與DE、FA、BC相交
則三個交點L、M、N三點共線
此定理也叫帕普斯定理
定理證明:
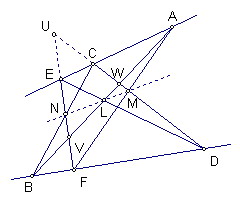
如圖,設直線CD與直線EF交於U
直線AB交直線CD、EF於W、V
運用Menelaus定理
△UVW有五條截線AF、BC、AC、BF、DE
可得以下五式
VL/LW*WD/DU*UE/EV=1......(1)
VA/AW*WM/MU*UF/FV=1......(2)
VB/BW*WC/CU*UN/NV=1......(3)
VA/AW*WC/CU*UE/EV=1......(4)
CB/BW*WD/DU*UF/FV=1......(5)
[(1)*(2)*(3)]/[(4)*(5)]可得
VL/LW*WM/MU*UN/NV=1
由Menelaus逆定理可得L、M、N三點共線
得證
全站熱搜


 留言列表
留言列表
