幾何寶庫

 

定理內容：
若兩個三角形對應頂點的連線共點
則其對應邊的交點共線
此定理也叫笛沙格定理、戴沙格定理

定理證明：

 

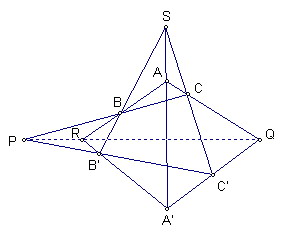
如圖，△ABC和△A'B'C'其對應頂點連線AA'、BB'、CC'交於一點S
BC與B'C'交於P、AC與A'C'交於Q、AB與A'B'交於R

由直線PB'C'截△SBC
由Menelaus定理有
BP/PC*CC'/C'S*SB'/B'B=1

同理由直線QC'A'截△SCA有
CQ/QA*AA'/A'S*SC'/C'C=1

由直線RB'A截△SAB有
AR/RB*BB'/B'S*SA'/A'A=1

以上三式相乘即得BP/PC*CQ/QA*AR/RB=1
由Menelaus逆定理得P、Q、R三點共線

得證


逆定理內容：
若兩個三角形對應邊的交點共線
則他們對應頂點的連線共點

逆定理證明：

  

如圖，△ABC和△A'B'C對應邊交點P、Q、R共線
BB直線、AA直線交於S

由直線SCC'截△SBC
由Menelaus定理有
QC'/C'A'*A'S/SA*AC/CQ=1

同理由直線PRQ截△A'B'C'有
A'C'/C'Q*QP/PR*RB'/B'A'=1

由直線PBC截△AQR有
AB/BR*RP/PQ*QC/CA=1

以上三式相乘有
RB'/B'A'*A'S/SA*AB/BR=1
由Menelaus逆定理得S、B、B'三點共線
即AA'、BB'、CC'交於一點S

得證