定理內容:
以三角形各邊為邊分別向外側作正三角形
則三個正三角形的中心構成一個正三角形
此定理也叫拿破崙定理
定理證明:
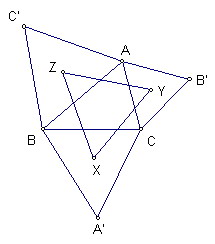
如圖△A'BC、△AB'C、△ABC'是以△ABC三邊向外作的三個正三角形
X、Y、Z分別為三正三角形的中心
連AA'、BB'、CC'
∵AB'=AC,AC'=AB,∠CAC'=∠BAB'
∴△BAB'全等於△C'AC(SAS)
→BB'=CC'
同理可得AA'=BB'
所以AA'=BB'=CC'
BZ=√3/3*AB,BX=√3/3*BC
∵BZ/BX=AB/BC=BC'/BC,∠ZBX=∠C'BC
∴△ZBX全等於△C'BC(SAS)
→XZ/CC'=√3/3
同理XY/AA'=YZ/BB'=√3/3
故XY=YZ=XZ
即△XYZ為正三角形
得證
全站熱搜


 留言列表
留言列表
