幾何寶庫

 

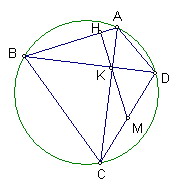
定理內容：
內接於圓的四邊形ABCD的對角線AC、BD垂直相交於K
過K的直線與AB、CD分別相交於H、M
(1)如果KH⊥AB,則MC=MD
(2)如果MC=MD,則KH⊥AB
此定理也叫婆羅摩及多定理、布拉美古塔定理

定理證明：

 

(1)
∵KH⊥AB、AC⊥BD
∴∠1=∠2=∠4
又∠2=∠3
所以∠3=∠4
→MC=MK
同理MD=MK
即MC=MD

得證

(2)
由MC=MD
得知KM為直角三角形CKD斜邊CD上中線
因此有MK=MC
→∠3=∠4
又∠3=∠2,∠4=∠1
所以∠2=∠1
而∠1+∠5=90°
所以∠2+∠5=90°
即KH⊥AB

得證


逆定理內容：
若四邊形的對角線互相垂直,並且
(1)過對角線交點向一邊所做垂線平分其對邊
(2)對角線交點與一邊中點的連線垂直於對邊
(3)對角線交點、交點在一邊上的射影及對邊中點三點共線
這三個中只要一個成立,則四邊形內接於圓

逆定理證明：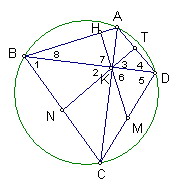

 

(1)
如圖,設KT⊥AD,KH⊥AB
HK、TK分別交CD、BC於M、N且M、N分別為CD、BC中點
則可得∠1=∠2=∠3,∠5=∠6=∠7

∵∠4+∠3=90°,∠8+∠7=90°
∴∠4+∠1=90°,∠8+∠5=90°
→∠CBA+∠CDA=180°
→四邊形ABCD內接於圓

得證

(2)
如圖，設M、N分別為CD、BC中點
MK、NK分別交AB、AD於H、T且KH⊥AB、KT⊥AD
則可得∠1=∠2=∠3,∠5=∠6=∠7

∵∠4+∠3=90°,∠8+∠7=90°
∴∠4+∠1=90°,∠8+∠5=90°
→∠CBA+∠CDA=180°
→四邊形ABCD內接於圓

得證

(3)
如圖，M、N分別為CD、BC中點、KH⊥AB、KT⊥AD
且T,K,N三點共線，H,K,M也三點共線
則可得∠1=∠2=∠3,∠5=∠6=∠7

∵∠4+∠3=90°,∠8+∠7=90°
∴∠4+∠1=90°,∠8+∠5=90°
→∠CBA+∠CDA=180°
→四邊形ABCD內接於圓

得證